How to use a Tide Curve problem
How to use a tide curve
This problem builds on our last tide problem.
We are repeating this type of problem to drive home the method of solving using a tide curve. If you got the last one wrong you can redeem your self esteem here. Before doing this one you should maybe look over the last one and the solution.
It’s a very similar problem just that you are passing the same point 5 or so weeks earlier.
Tidal Exercise
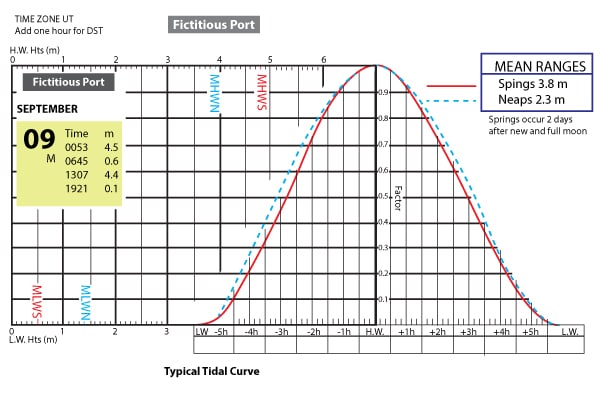
On Monday September 9th you are going to sail past this fictitious port in the morning. There is a shallow area you’d like to pass over. The tidal information you have obtained is as such below with the accompanying tide curve for this port.
The chart says the depth of the water of the shallow area is 1 meter. You draw one and a half meters and you would like 1 meter below the keel for safety. Summer daylight savings is in effect. A couple of nights ago you noticed a new moon.
(click image for downloadable PDF)
According to your requirements of 1 meter clearance below the keel, what times in the morning is it safe to traverse the shallow area?
Please try to solve the answer yourself first before cruising the answer. Give it a go – come one.
ANSWER
Really? Did you give it a go first?
You need 2.5 meters of water depth. The chart says it is 1 meter at MLLW. So this means the tide needs to be 1.5 meters or higher. The answer lies in when will the tide be 1.5 meters and above?
Daylight savings is in effect and the chart above says add 1 hour to the times to get DST. The times then, should be adjusted as such:
0153: 4.5m
0745: 0.6 m
1407: 4.4 m
2021: 0.1 m
Since low tide is 0.6 meters this is lower than the requirement. The depth of the water at this time would only be 1.6 meters. Chart datum plus tide height. So the times for transit in the morning are anywhere from midnight until a time whereby the ebbing (dropping) tide is 1.5 meters (this will be before 7:45) and some time after 7:45 where the flooding (rising) tide returns back to 1.5 meters.
First look at the ebbing tide curve. The range of tide is 0.6 low and 4.5 high. The high occurs at 0153. Since you noticed a new moon a few days ago and the range of tide from low to high matches a spring tide, use the spring tide sinusoidal shape curve. First enter the high tide time and each hour after that. Now, bring a line down from the 1.5 meter requirement to the sloped line on the left. Bring it across to the falling tide curve and then down to the time. At 0553 the tide will have dropped to 1.5 meters and you can not traverse after this time until the tide comes back up to 1.5 meters on its next rise.
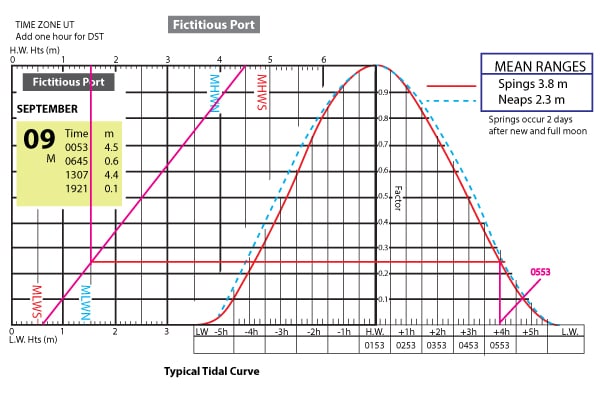
Falling tide from 0153 through 0745
To solve the next time, redo the curve for the flooding tide. The range is 0.6 meters low to 4.4 meters high. Again, find when it has risen to 1.5 meters. On the image, enter in the high tide time and the hours prior. Now bring a line down from 1.5 meters to the sloped line and across to the rising tide curve spring line. Drop that down tot he time scale. You find that after 1017 the tide has risen back to 1.5 meters and you can transit any time after this.
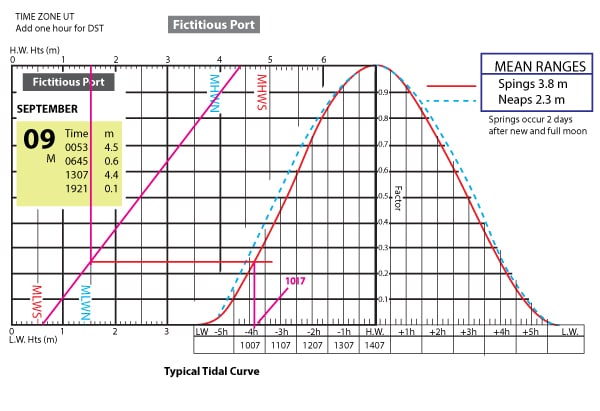
Flooding tide from 0.6 m to 4.4 m tide curve.
The answer is before 0553 and after 1017.
As in the previous example, we posted some things to be wary of in following this exactly. There are other factors you should think about for real like waves, wind, atmospheric pressure, shifting sand bars, accuracy of your depth meter, ability to stay on course on the chart, updated chart info may exist, etc. Additionally you should probably give yourself an additional time safety factor like 20 minutes or so. Be conservative in your approach.
NauticEd International Sailing Education courses are eLearning, multimedia courses designed to help you to be a safe and knowledgeable sailor. If you didn’t know how to solve this problem, you should be signing up for our courses.
Start by taking the NauticEd Skipper course. We hope you enjoyed this problem.
- Getting a Sailing Qualification while on a Sailing Vacation - April 24, 2024
- RYA Day Skipper with NauticEd - April 1, 2024
- NauticEd uses the SailTies GPS Tracking App - March 29, 2024